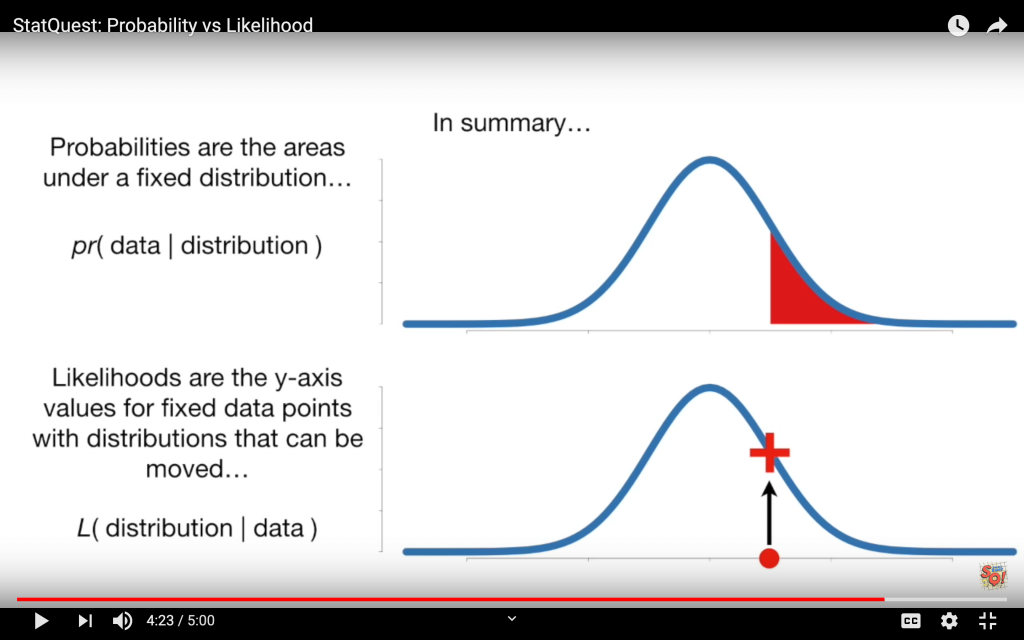
The difference between probability and likelihood is central, among others, to understanding MLE. Randy Gallistel has posted a succinct treatment of this topic:
The distinction between probability and likelihood is fundamentally important: Probability attaches to possible results; likelihood attaches to hypotheses [my emphasis]. Explaining this distinction is the purpose of this first column.
Possible results [ie. probabilites] are mutually exclusive and exhaustive. Suppose we ask a subject to predict the outcome of each of 10 tosses of a coin. There are only 11 possible results (0 to 10 correct predictions). The actual result will always be one and only one of the possible results. Thus, the probabilities that attach to the possible results must sum to 1.
Hypotheses, unlike results, are neither mutually exclusive nor exhaustive. Suppose that the first subject we test predicts 7 of the 10 outcomes correctly. I might hypothesize that the subject just guessed, and you might hypothesize that the subject may be somewhat clairvoyant, by which you mean that the subject may be expected to correctly predict the results at slightly greater than chance rates over the long run. These are different hypotheses, but they are not mutually exclusive, because you hedged when you said “may be.” You thereby allowed your hypothesis to include mine. In technical terminology, my hypothesis is nested within yours. Someone else might hypothesize that the subject is strongly clairvoyant and that the observed result underestimates the probability that her next prediction will be correct. Another person could hypothesize something else altogether. There is no limit to the hypotheses one might entertain.
The set of hypotheses to which we attach likelihoods is limited by our capacity to dream them up. In practice, we can rarely be confident that we have imagined all the possible hypotheses. Our concern is to estimate the extent to which the experimental results affect the relative likelihood of the hypotheses we and others currently entertain. Because we generally do not entertain the full set of alternative hypotheses and because some are nested within others, the likelihoods that we attach to our hypotheses do not have any meaning in and of themselves; only the relative likelihoods — that is, the ratios of two likelihoods — have meaning.
[…] To decide which of two hypotheses is more likely given an experimental result, we consider the ratios of their likelihoods. This ratio, the relative likelihood ratio, is called the “Bayes Factor.”
Josh Starmer from StatQuest explains the same concept in a different way: